This part also is from Chapter 4.1.2 (SDR4Engineers)

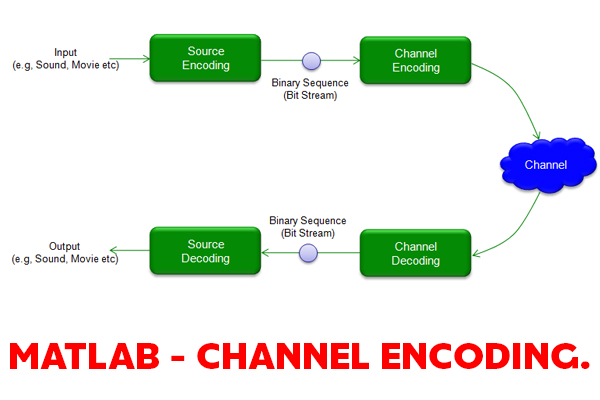
To protect a digital transmission from the possibility of its information being corrupted, it is necessary to introduce some level of controlled redundancy in order to reverse the effects of data corruption. Consequently, channel encoding is designed to correct for channel transmission errors by introducing controlled redundancy into the data transmission. As opposed to the redundancy that is removed during the source encoding process, which is random in nature, the redundancy introduced by a channel encoding is specifically designed to combat the effects of bit errors in the transmission (i.e., the redundancy possesses a specific structure known to both the transmitter and receiver).

In general, channel encoding operates as follows: Each vector of a source encoded output of length K ; namely, v_{l} where l=1,2, \ldots, 2^{K}, is assigned a unique codeword such that the vector v_{l}=(101010 \ldots) is assigned a unique codeword c_{l} \in \mathbb{C} of length N, where \mathbb{C} is a codebook.

When designing a codebook for a channel encoder, it is necessary to quantitatively assess how well or how poorly the codewords will perform in a situation involving data corruption. Consequently, the Hamming distance is often used to determine the effectiveness of a set of codewords contained within a codebook by evaluating the relative difference between any two codewords. For example, suppose we have a codebook consisting of \{101,010\}. We can readily calculate the minimum Hamming distance to be equal to d_{H, \min }=3, which is the best possible result. On the other hand, a codebook consisting of \{111,101\} possesses a minimum Hamming distance of d_{H, \min }=1, which is relatively poor in comparison to the previous codebook example. (For more information, please google it 🙂 )

Code explanation: Let us apply repetition coding to an actual vector, using a range of repetition rates, and observe its impact when the binary vector is exposed to random bit-flips. The MATLAB script below takes the original binary vector bin_str and introduces controlled redundancy into it in the form of repeating these binary values by a factor of N. For example, instead of transmitting 010, applying a repetition coding scheme with a repetition factor of N = 3 would yield an output of 000111000. The reason this is important is that in the event a bit is flipped from a one to a zero or from a zero to a one, which is considered an error, the other repeated bits could be used to nullify the error at the receiver.

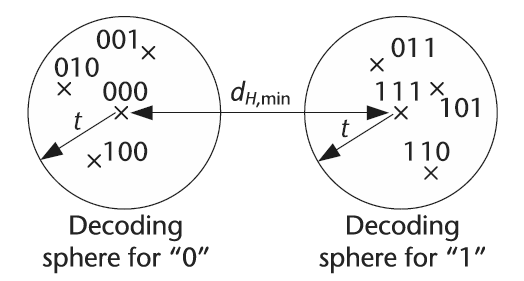
Hamming distance visualization.

A rate 1/3 repetition code with no source encoding would look like:

    \[ \begin{aligned} 1 \rightarrow & 111=c_{1}(1 \text { st codeword }) \\ 0 \rightarrow & 000=c_{2}(2 \text { nd codeword }) \\ & \therefore C=\{000,111\} \end{aligned} \]

The output:

More redundancy, less BER