A long time since I posted the last time… I have been studying new topics. Today, I’d like to share a post about a DSP function on ARM processors. It is “convolution.”
Let’s begin with the definition. I can say that the magic keyword behind the convolution is “signal decomposition”. You should investigate their relationship. Also, you can also check out this chapter or this series. They describe the connection between impulse response and convolution function in a nutshell. I merely provide you with the source because I don’t have enough time to explain them from scratch or to make them animated.
Here is the discrete equation of the convolution:
![\[y[n]=h[n]{ }^{*} x[n]\]](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-86eae0519e0ab3a9027b9fef42fc4da9_l3.svg "Rendered by QuickLaTeX.com")
![\mathrm{x}[\mathrm{n}]: N](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-eeecd430fb9471ff7581fd030676f301_l3.svg "Rendered by QuickLaTeX.com")
-point signal from 0 to 
![\mathrm{h}[\mathrm{n}]](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-3ba00cda96799decaf71cbb152e0d0ba_l3.svg "Rendered by QuickLaTeX.com")
: 
-point signal from 0 to -1![\mathrm{h}[\mathrm{n}]{*}\mathrm{x}[\mathrm{n}]: N+M-2](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-760014df9e844c97664766ca3a3f5c3d_l3.svg "Rendered by QuickLaTeX.com")
point signal from 0 to 
![\[y[i]=\sum_{j=0}^{M-1} h[j] x[\mathrm{i-j}]\]](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-d7f65c6f9dbfa997d0360aed27468189_l3.svg "Rendered by QuickLaTeX.com")
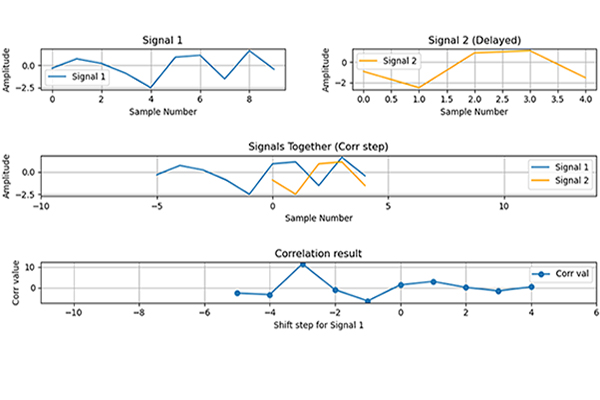
Let’s analyze a specific output point, how does it calculated…
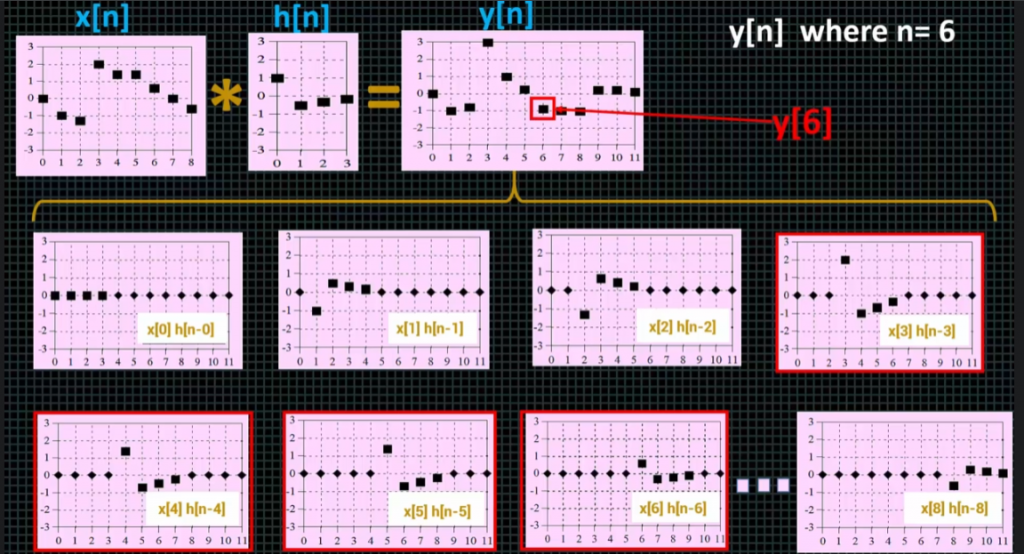
As can be seen from the explanation above, we can decompose the output signal to decide which scale/shift step of impulse response affects the 6th element at the output. The pattern can be seen clearly!
![y[n]= x[3]h[n-3] + x[4]h[n-4] + x[5]h[n-5] + x[6]h[n-6]](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-58b326765b12678caf2b891699030888_l3.svg "Rendered by QuickLaTeX.com")
![y[6]= x[3]h[6-3] + x[4]h[6-4] + x[5]h[6-5] + x[6]h[6-6]](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-7bf78311f1da18115505e23d731130db_l3.svg "Rendered by QuickLaTeX.com")
![y[6]= x[3]h[3] + x[4]h[2] + x[5]h[1] + x[6]h[0]](https://unalfaruk.com/wp-content/ql-cache/quicklatex.com-67ba9f411f70cf81e74a1368754570ef_l3.svg "Rendered by QuickLaTeX.com")
So, the sum of i and j values which are index values of the input signal and the impulse response must be the same as the index value of the output signal which we’re analyzing. It is our algorithm…
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| #include "stm32wlxx_hal.h" | |
| #include "arm_math.h" // ARM::CMSIS:DSP | |
| #define SIG_LENGTH 250 | |
| #define IMP_RSP_LEN 29 | |
| #define NUM_TAPS 29 | |
| #define BLOCK_SIZE 32 | |
| uint32_t freq; //it is just for trace.. not related to DSP | |
| extern void SystemClock_Config(void); | |
| extern float32_t inputSignal_f32_1kHz_15kHz[SIG_LENGTH]; | |
| void plot_input_signal(void); | |
| void plot_imp_response(void); | |
| void convolution(float32_t * sig_in, uint32_t len_sig_in, float32_t * imp_response, uint32_t len_imp_response, float32_t * sig_out); | |
| void plot_output_signal(void); | |
| void plot_all(void); | |
| float32_t outputSignal[IMP_RSP_LEN+SIG_LENGTH]; | |
| // Impulse reponse signal for low-pass filter | |
| const float32_t impulseResponse[IMP_RSP_LEN] = { | |
| -0.0018225230f, -0.0015879294f, +0.0000000000f, +0.0036977508f, +0.0080754303f, +0.0085302217f, -0.0000000000f, -0.0173976984f, | |
| -0.0341458607f, -0.0333591565f, +0.0000000000f, +0.0676308395f, +0.1522061835f, +0.2229246956f, +0.2504960933f, +0.2229246956f, | |
| +0.1522061835f, +0.0676308395f, +0.0000000000f, -0.0333591565f, -0.0341458607f, -0.0173976984f, -0.0000000000f, +0.0085302217f, | |
| +0.0080754303f, +0.0036977508f, +0.0000000000f, -0.0015879294f, -0.0018225230f | |
| }; | |
| float32_t inputSample, impResponseSample, outputSample; | |
| int main(){ | |
| int i; | |
| HAL_Init(); | |
| SystemClock_Config(); | |
| freq=HAL_RCC_GetHCLKFreq(); //it is just for trace.. not related to DSP | |
| convolution((float32_t *)&inputSignal_f32_1kHz_15kHz[0], (uint32_t) SIG_LENGTH, (float32_t *)&impulseResponse[0], (uint32_t)IMP_RSP_LEN, (float32_t *)&outputSignal[0]); | |
| HAL_Delay(1); | |
| // plot_input_signal(); | |
| // HAL_Delay(1); | |
| // plot_imp_response(); | |
| // HAL_Delay(1); | |
| // plot_output_signal(); | |
| plot_all(); | |
| while(1) | |
| { | |
| } | |
| } | |
| // Plotting the input signal on the logic analyzer in Keil | |
| void plot_input_signal(void) | |
| { | |
| int i, j; | |
| for (i=0;i<SIG_LENGTH;i++){ | |
| inputSample=inputSignal_f32_1kHz_15kHz[i]; | |
| for(j=0;j<3000;j++){} | |
| //if(i==SIG_LENGTH-1) i=0; | |
| } | |
| } | |
| // Plotting the impulse response signal on the logic analyzer in Keil | |
| void plot_imp_response(void) | |
| { | |
| int i, j; | |
| for (i=0;i<IMP_RSP_LEN;i++){ | |
| impResponseSample=impulseResponse[i]; | |
| for(j=0;j<3000;j++){} | |
| //if(i==SIG_LENGTH-1) i=0; | |
| } | |
| } | |
| // Plotting only output signal on the logic analyzer in Keil | |
| void plot_output_signal(void) | |
| { | |
| int i, j; | |
| for (i=0;i<IMP_RSP_LEN+SIG_LENGTH;i++){ | |
| outputSample=outputSignal[i]; | |
| for(j=0;j<3000;j++){} | |
| //if(i==IMP_RSP_LEN+SIG_LENGTH-1) i=0; | |
| } | |
| } | |
| // Plotting all signals on the logic analyzer in Keil | |
| void plot_all(void){ | |
| int i,j,g,k; | |
| i=j=0; | |
| for(k=0;k<(SIG_LENGTH+IMP_RSP_LEN);k++){ | |
| i++; | |
| j++; | |
| if(i<SIG_LENGTH) inputSample = inputSignal_f32_1kHz_15kHz[i]; | |
| if(j<IMP_RSP_LEN) impResponseSample = impulseResponse[j]; | |
| if(k<IMP_RSP_LEN+SIG_LENGTH-1) outputSample = outputSignal[k]; | |
| for(g=0;g<20000;g++){} | |
| } | |
| } | |
| // Convolution function | |
| void convolution(float32_t * sig_in, uint32_t len_sig_in, float32_t * imp_response, uint32_t len_imp_response, float32_t * sig_out){ | |
| uint16_t i,j; | |
| for(i=0;i<(len_sig_in+len_imp_response);i++) | |
| { | |
| sig_out[i]=0; | |
| } | |
| for(i=0;i<len_sig_in;i++) | |
| { | |
| for(j=0;j<len_imp_response;j++) | |
| { | |
| sig_out[i+j] = sig_out[i+j]+sig_in[i]*imp_response[j]; | |
| } | |
| } | |
| } | |
| void SysTick_Handler(void){ | |
| HAL_IncTick(); | |
| HAL_SYSTICK_IRQHandler(); | |
| } |
by
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| #include "arm_math.h" // ARM::CMSIS:DSP | |
| float32_t inputSignal_f32_1kHz_15kHz[320] = | |
| { | |
| +0.0000000000f, +0.5924659585f, -0.0947343455f, +0.1913417162f, +1.0000000000f, +0.4174197128f, +0.3535533906f, +1.2552931065f, | |
| +0.8660254038f, +0.4619397663f, +1.3194792169f, +1.1827865776f, +0.5000000000f, +1.1827865776f, +1.3194792169f, +0.4619397663f, | |
| +0.8660254038f, +1.2552931065f, +0.3535533906f, +0.4174197128f, +1.0000000000f, +0.1913417162f, -0.0947343455f, +0.5924659585f, | |
| -0.0000000000f, -0.5924659585f, +0.0947343455f, -0.1913417162f, -1.0000000000f, -0.4174197128f, -0.3535533906f, -1.2552931065f, | |
| -0.8660254038f, -0.4619397663f, -1.3194792169f, -1.1827865776f, -0.5000000000f, -1.1827865776f, -1.3194792169f, -0.4619397663f, | |
| -0.8660254038f, -1.2552931065f, -0.3535533906f, -0.4174197128f, -1.0000000000f, -0.1913417162f, +0.0947343455f, -0.5924659585f, | |
| +0.0000000000f, +0.5924659585f, -0.0947343455f, +0.1913417162f, +1.0000000000f, +0.4174197128f, +0.3535533906f, +1.2552931065f, | |
| +0.8660254038f, +0.4619397663f, +1.3194792169f, +1.1827865776f, +0.5000000000f, +1.1827865776f, +1.3194792169f, +0.4619397663f, | |
| +0.8660254038f, +1.2552931065f, +0.3535533906f, +0.4174197128f, +1.0000000000f, +0.1913417162f, -0.0947343455f, +0.5924659585f, | |
| +0.0000000000f, -0.5924659585f, +0.0947343455f, -0.1913417162f, -1.0000000000f, -0.4174197128f, -0.3535533906f, -1.2552931065f, | |
| -0.8660254038f, -0.4619397663f, -1.3194792169f, -1.1827865776f, -0.5000000000f, -1.1827865776f, -1.3194792169f, -0.4619397663f, | |
| -0.8660254038f, -1.2552931065f, -0.3535533906f, -0.4174197128f, -1.0000000000f, -0.1913417162f, +0.0947343455f, -0.5924659585f, | |
| +0.0000000000f, +0.5924659585f, -0.0947343455f, +0.1913417162f, +1.0000000000f, +0.4174197128f, +0.3535533906f, +1.2552931065f, | |
| +0.8660254038f, +0.4619397663f, +1.3194792169f, +1.1827865776f, +0.5000000000f, +1.1827865776f, +1.3194792169f, +0.4619397663f, | |
| +0.8660254038f, +1.2552931065f, +0.3535533906f, +0.4174197128f, +1.0000000000f, +0.1913417162f, -0.0947343455f, +0.5924659585f, | |
| +0.0000000000f, -0.5924659585f, +0.0947343455f, -0.1913417162f, -1.0000000000f, -0.4174197128f, -0.3535533906f, -1.2552931065f, | |
| -0.8660254038f, -0.4619397663f, -1.3194792169f, -1.1827865776f, -0.5000000000f, -1.1827865776f, -1.3194792169f, -0.4619397663f, | |
| -0.8660254038f, -1.2552931065f, -0.3535533906f, -0.4174197128f, -1.0000000000f, -0.1913417162f, +0.0947343455f, -0.5924659585f, | |
| -0.0000000000f, +0.5924659585f, -0.0947343455f, +0.1913417162f, +1.0000000000f, +0.4174197128f, +0.3535533906f, +1.2552931065f, | |
| +0.8660254038f, +0.4619397663f, +1.3194792169f, +1.1827865776f, +0.5000000000f, +1.1827865776f, +1.3194792169f, +0.4619397663f, | |
| +0.8660254038f, +1.2552931065f, +0.3535533906f, +0.4174197128f, +1.0000000000f, +0.1913417162f, -0.0947343455f, +0.5924659585f, | |
| -0.0000000000f, -0.5924659585f, +0.0947343455f, -0.1913417162f, -1.0000000000f, -0.4174197128f, -0.3535533906f, -1.2552931065f, | |
| -0.8660254038f, -0.4619397663f, -1.3194792169f, -1.1827865776f, -0.5000000000f, -1.1827865776f, -1.3194792169f, -0.4619397663f, | |
| -0.8660254038f, -1.2552931065f, -0.3535533906f, -0.4174197128f, -1.0000000000f, -0.1913417162f, +0.0947343455f, -0.5924659585f, | |
| +0.0000000000f, +0.5924659585f, -0.0947343455f, +0.1913417162f, +1.0000000000f, +0.4174197128f, +0.3535533906f, +1.2552931065f, | |
| +0.8660254038f, +0.4619397663f, +1.3194792169f, +1.1827865776f, +0.5000000000f, +1.1827865776f, +1.3194792169f, +0.4619397663f, | |
| +0.8660254038f, +1.2552931065f, +0.3535533906f, +0.4174197128f, +1.0000000000f, +0.1913417162f, -0.0947343455f, +0.5924659585f, | |
| +0.0000000000f, -0.5924659585f, +0.0947343455f, -0.1913417162f, -1.0000000000f, -0.4174197128f, -0.3535533906f, -1.2552931065f, | |
| -0.8660254038f, -0.4619397663f, -1.3194792169f, -1.1827865776f, -0.5000000000f, -1.1827865776f, -1.3194792169f, -0.4619397663f, | |
| -0.8660254038f, -1.2552931065f, -0.3535533906f, -0.4174197128f, -1.0000000000f, -0.1913417162f, +0.0947343455f, -0.5924659585f, | |
| -0.0000000000f, +0.5924659585f, -0.0947343455f, +0.1913417162f, +1.0000000000f, +0.4174197128f, +0.3535533906f, +1.2552931065f, | |
| +0.8660254038f, +0.4619397663f, +1.3194792169f, +1.1827865776f, +0.5000000000f, +1.1827865776f, +1.3194792169f, +0.4619397663f, | |
| +0.8660254038f, +1.2552931065f, +0.3535533906f, +0.4174197128f, +1.0000000000f, +0.1913417162f, -0.0947343455f, +0.5924659585f, | |
| +0.0000000000f, -0.5924659585f, +0.0947343455f, -0.1913417162f, -1.0000000000f, -0.4174197128f, -0.3535533906f, -1.2552931065f, | |
| -0.8660254038f, -0.4619397663f, -1.3194792169f, -1.1827865776f, -0.5000000000f, -1.1827865776f, -1.3194792169f, -0.4619397663f, | |
| -0.8660254038f, -1.2552931065f, -0.3535533906f, -0.4174197128f, -1.0000000000f, -0.1913417162f, +0.0947343455f, -0.5924659585f, | |
| -0.0000000000f, +0.5924659585f, -0.0947343455f, +0.1913417162f, +1.0000000000f, +0.4174197128f, +0.3535533906f, +1.2552931065f, | |
| +0.8660254038f, +0.4619397663f, +1.3194792169f, +1.1827865776f, +0.5000000000f, +1.1827865776f, +1.3194792169f, +0.4619397663f, | |
| +0.8660254038f, +1.2552931065f, +0.3535533906f, +0.4174197128f, +1.0000000000f, +0.1913417162f, -0.0947343455f, +0.5924659585f, | |
| +0.0000000000f, -0.5924659585f, +0.0947343455f, -0.1913417162f, -1.0000000000f, -0.4174197128f, -0.3535533906f, -1.2552931065f, | |
| }; |
The signals on the logic analyzer:
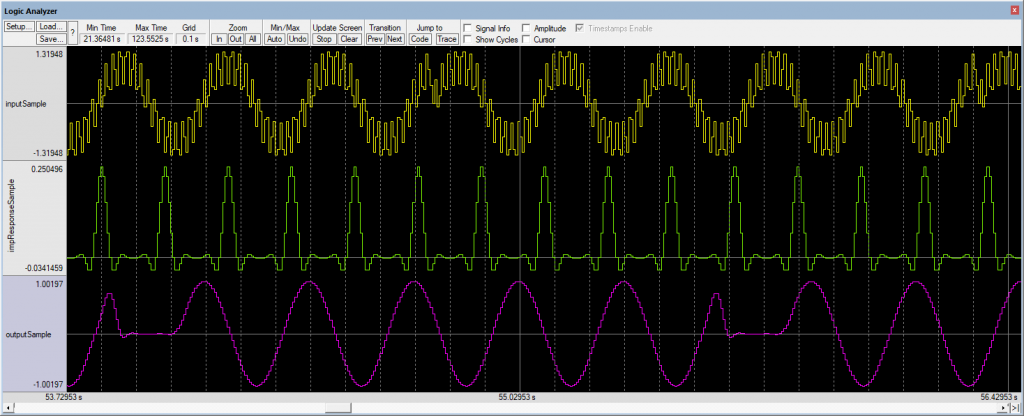
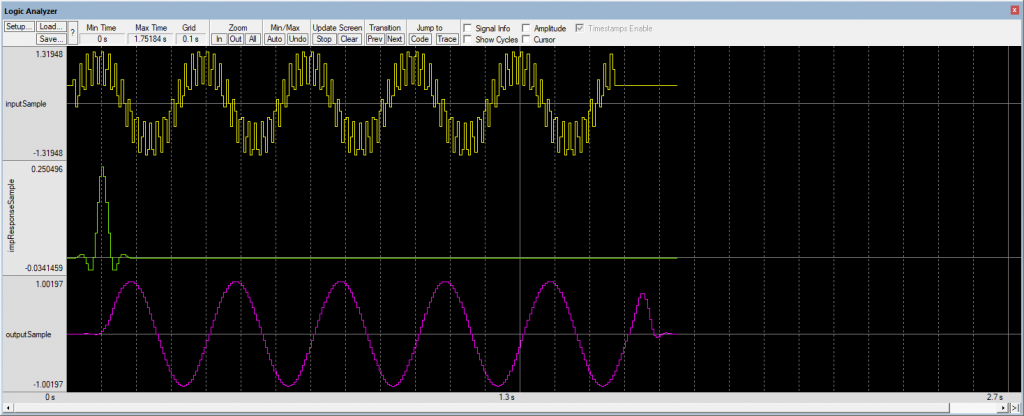
It’s the first part of the post… CMSIS Convolution will be described and implemented in the next post…
I am waiting for your feedback… tips and tricks, or my faults, etc.
Leave a Reply