The Variance Sum Law…

When I was working on a simulation project two or three months ago, there were a few arithmetic problems relating to statistical concepts like variance, standard deviation, etc. For a new feature that we would like to implement in the simulation, I had to perform a few mathematical operations on the variances of a few random variables such as calculating the sum, mean, and total of variances. But I did not know the math behind it…

I did some research about it. In the communities, I saw a few various strategies. I now understand the notion and the process involved. I really would like to share my experience with people who may someday require it.

A StackExchange thread is my main resource, which I’ll provide now. Here is the URL. And my favorite approach is the one below:

Please read the initial sections of the book “Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches” if you have trouble understanding the equations or don’t know what the letters in them represent.

Let’s design and run a simulation together to investigate the concept. There will be two random variables with different variances, and a basic sum operator to add each pair of random variables.

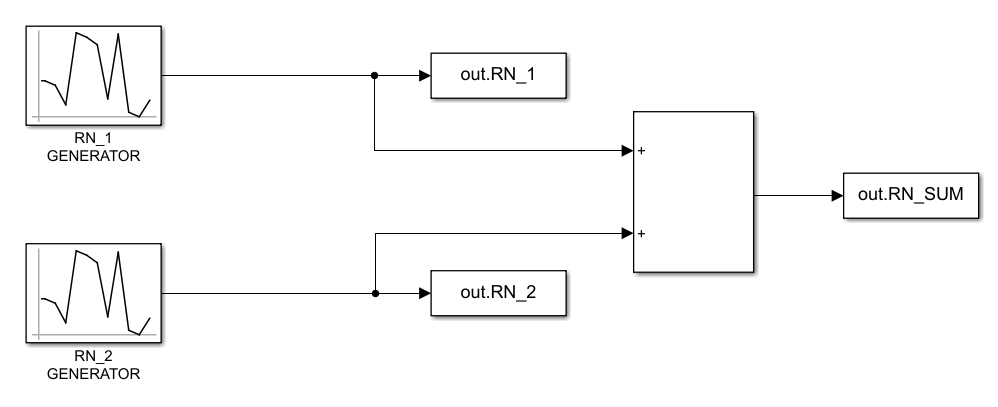
We expect that the variance of the sum operator’s output will equal the sum of all variances. Let’s run the simulation, and analyze the result… But before, let me show you the simulation parameters…

%SIMULATION PARAMETERS
modelDuration = 200;
setVar_RN_1 = 100;
setVar_RN_2 = 256;
setMean_RN_1 = 0;
setMean_RN_2 = 0;
setSeed_RN_1 = 0;
setSeed_RN_2 = 0;

The output variance is expected to be around 356, based on the above parameters.

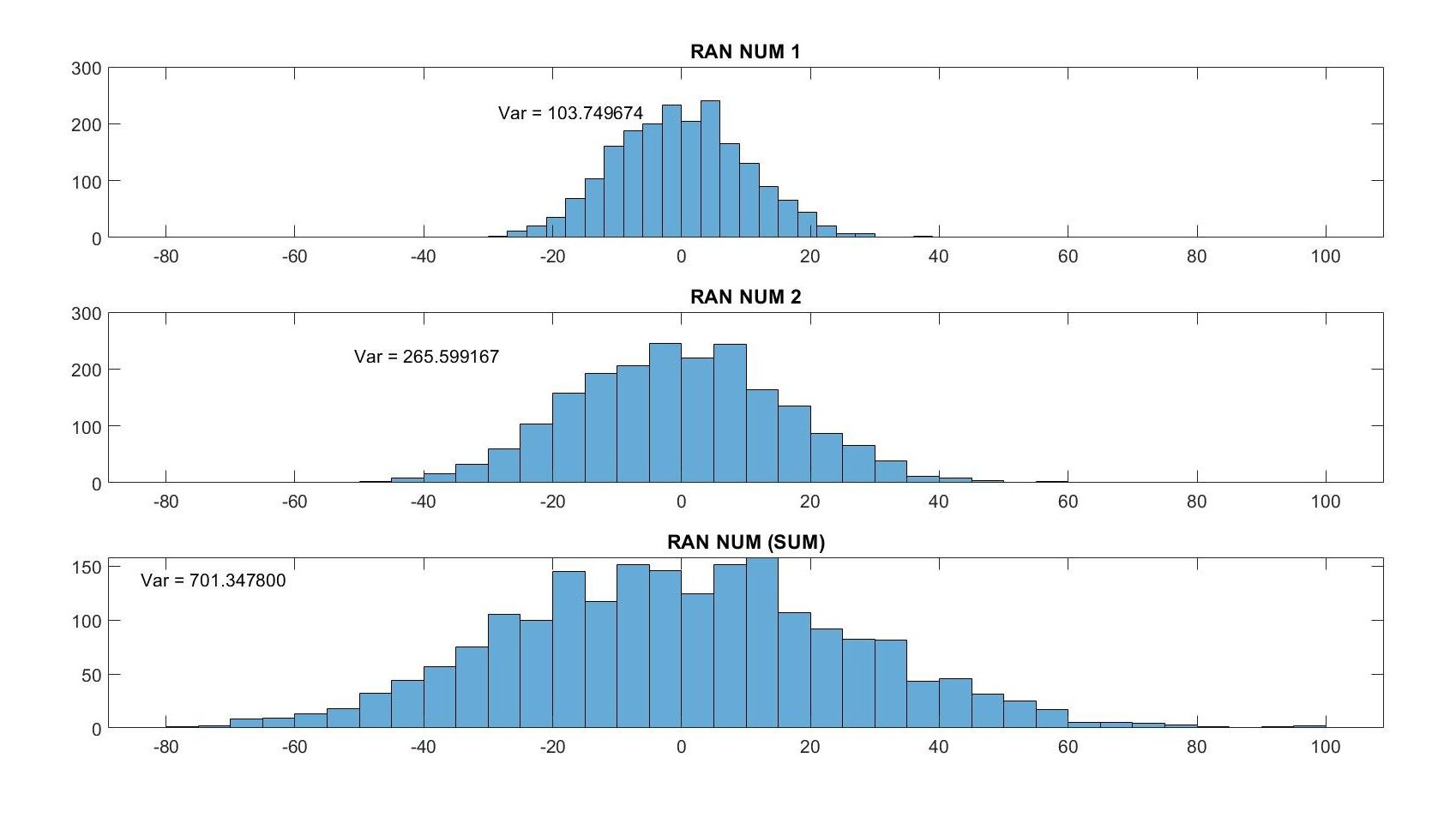
But it is by no means near! So? Let’s look at the equation above (also you can look at the StackExchange URL above). In the context of the description above, the sum of variance law behaves differently and contains additional values if two random variables are not independent. How can we determine whether or not the values are independent? The ket is covariance!

Let’s look at it…

cov(out.RN_1, out.RN_2)

ans =

  103.7497  165.9995
  165.9995  265.5992

As can be seen above, the covariance is neither exact zero nor almost zero. It means that the two variables are not independent. Then, how can we produce two independent values? The key is ‘seed’…

As can be seen in the SIMULINK model, we have two random number generator blocks. These blocks have “seed” parameters in their configuration. Although it affects the randomness between the generators, I am not an expert enough to describe how it is exactly, unfortunately. Please review the reference documents of it; however, I was not satisfied enough with that explanation.

Let’s change the seed values.

%SIMULATION PARAMETERS
modelDuration = 200;
setVar_RN_1 = 100;
setVar_RN_2 = 256;
setMean_RN_1 = 0;
setMean_RN_2 = 0;
setSeed_RN_1 = 1234;
setSeed_RN_2 = 4321;

Let’s run and look at the result…

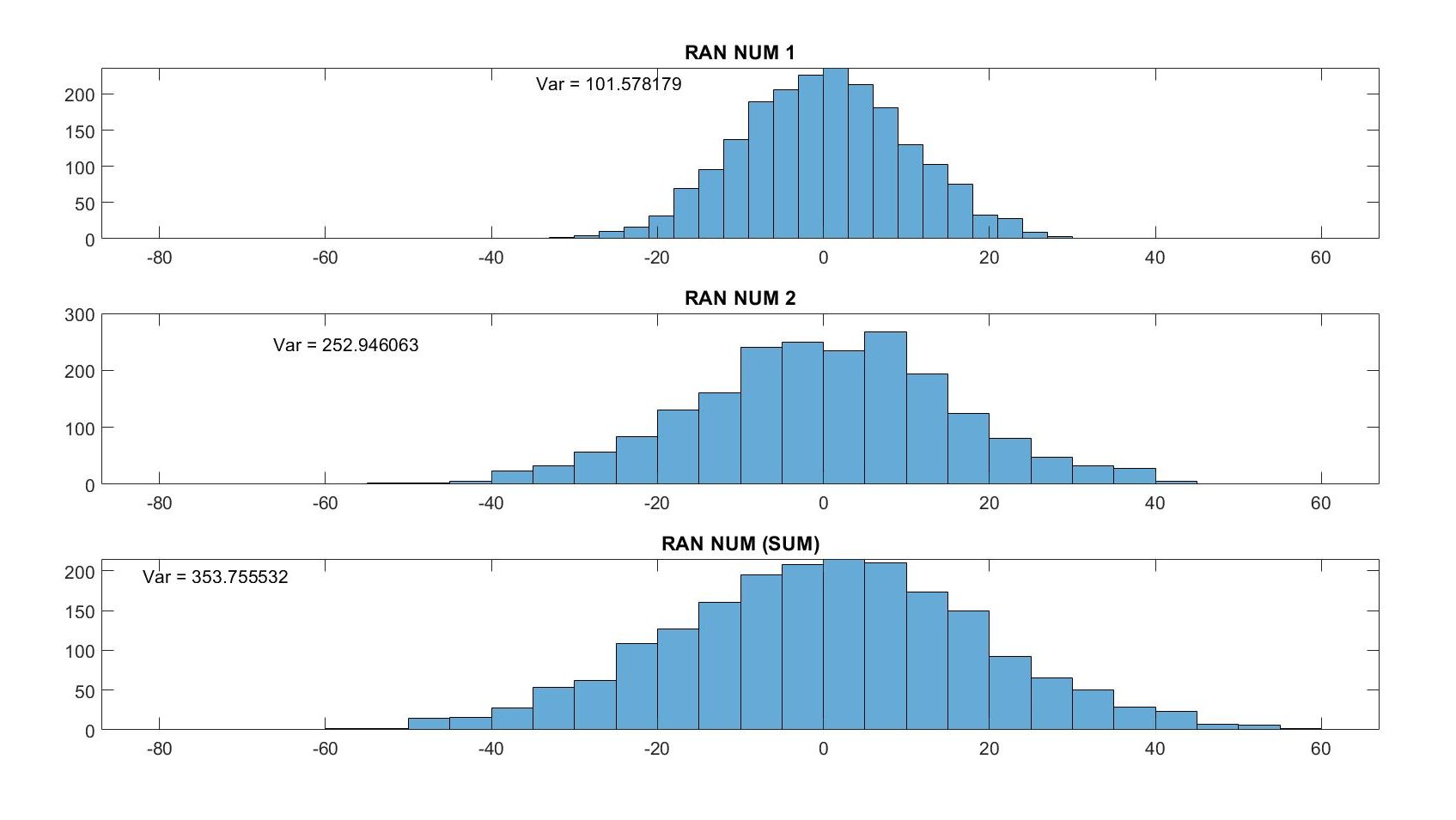
Perfect! Expected result! Let’s be sure about the covariance…

cov(out.RN_1, out.RN_2)

ans =

  101.5782   -0.3844
   -0.3844  252.9461

As can be seen above, the covariance is almost zero. It means that the two variables are independent. And, the law is working…

CONCLUSION

The law is working but behaves differently depending on the independence(covariance) status of the variables.

• Dependent Random Variables: The sum of the variances for two random variables does not equal the total variance, but more.
• Independent Random Variables: The variance of the sum is the sum of the variances.

Here are the SIMULINK and MATLAB files…