We’ll look at the doppler effect today—the impact of speed on a signal. As you can see from the “about me” section, my master’s thesis focused on satellite navigation technologies, and it is an important factor in satellite navigation. Now that I’ve digested it, I’d like to explain the fundamentals of the concept with a simple code implementation.
If you do not know what the “Doppler Effect” is or you would like to recall it, please look at the Wikipedia page. It’s a good reference this time for the topic. I would like to share just the logic and its implementation in a programming language.
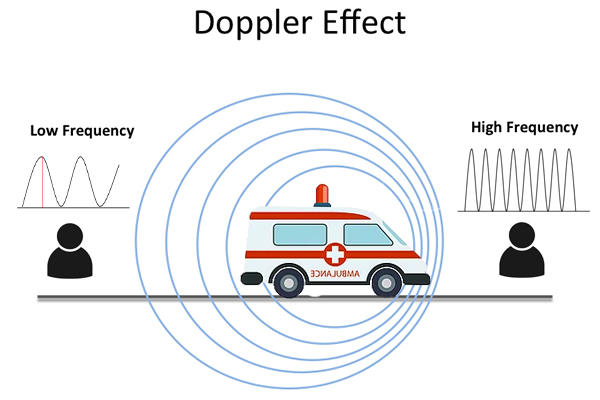
Whenever you hear a beacon on a car, you probably recognize that the pitch of sound varies. Have you ever thought about the reason? Let me explain basically.
All signals consist of waves(the type differs). And these waves have some characteristics such as frequency and wavelength. When a source of sound or light is moving relative to an observer, the frequency of the wave will vary as a result, an effect known as the Doppler effect or Doppler shift. Maybe this short video on YouTube can help you better understand how waves behave in a visual animation.
Here is the math behind it:
![]()
 is the propagation speed of waves in the medium;
is the propagation speed of waves in the medium;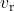 is the speed of the receiver relative to the medium, added to {\displaystyle c}
is the speed of the receiver relative to the medium, added to {\displaystyle c}if the receiver is moving towards the source, subtracted if the receiver is moving away from the source;
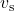 is the speed of the source relative to the medium, added to
is the speed of the source relative to the medium, added to  if the source is moving away from the receiver, subtracted if the source is moving towards the receiver.
if the source is moving away from the receiver, subtracted if the source is moving towards the receiver.
For example;
 is the propagation speed of waves in the medium;
is the propagation speed of waves in the medium;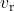 = 0;
= 0;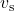 = 35 m/s, moving towards the receiver.
= 35 m/s, moving towards the receiver.- Beacon freq = 500 Hz
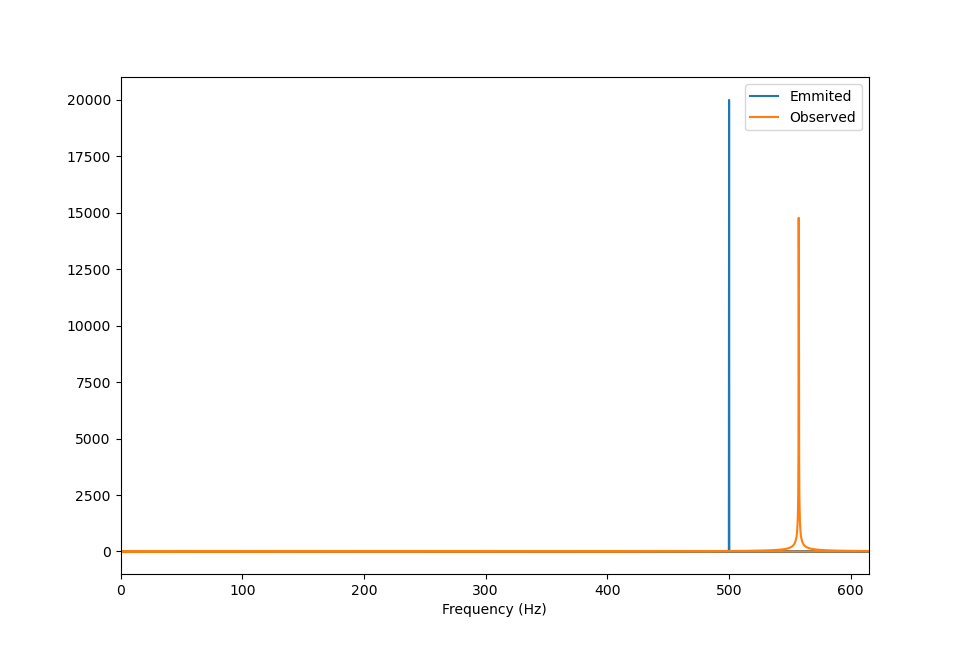
Beacon freq= 500.000000
Observer freq= 557.283142For satellite navigation, just change the values of the parameters in the equation. Especially the constant “c”… it won’t be a sound wave, it will be a radio wave.

Leave a Reply