SoftGNSS | postProcessing – Tracking

In the last post, we acquired the signals from GNSS satellites. Now we will keep tracking these signals to demodulate the navigation data continuously.

The signal transmitted by a satellite is:

is C/A code sequence,
is P(Y) code sequence,
is P(Y) navigation data sequence,
is power.

We need to extract the data from the signal above. So downconversion, band/low pass filters, etc. are used. Basically, the diagram below is used;

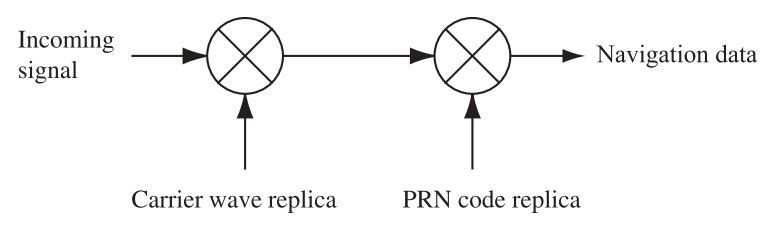
The output from the front end including filtering and downconversion can be described as

where is the intermediate frequency.

Then the signal is sampled by the A/D converter. Because of the narrow bandpass filter around the C/A code, the P code is distorted. The signal from satellite can be shown as:

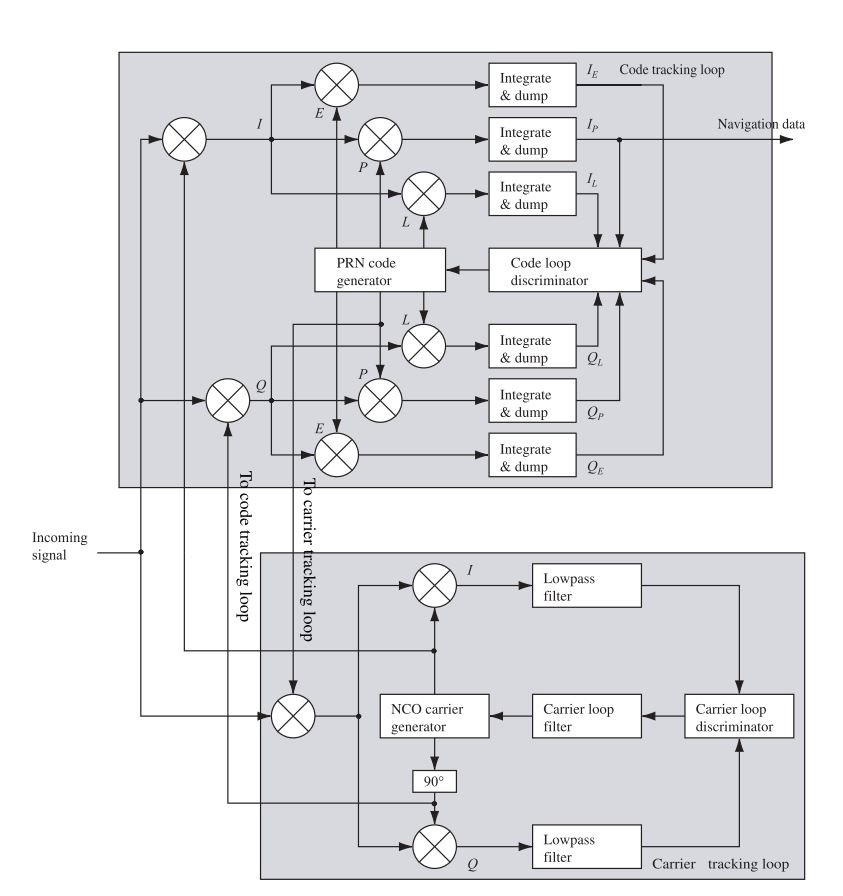
To get the from the signal above, the signal is converted to baseband by carrier removal.

Now, the second term is removed by lowpass filter. The rest term is multiplication of the nav message and PRN code.

The next and last step is removing the PRN code from the signal.

The demodulation above is only for a signal with one satellite. This is done to reduce the complexity, to explain the theory and to give a simpler idea of the demodulation scheme.

SoftGNSSv3 that I use…